realtorer.blogg.se

You'll notice that in the programĭescription, we are told that the "solution that it

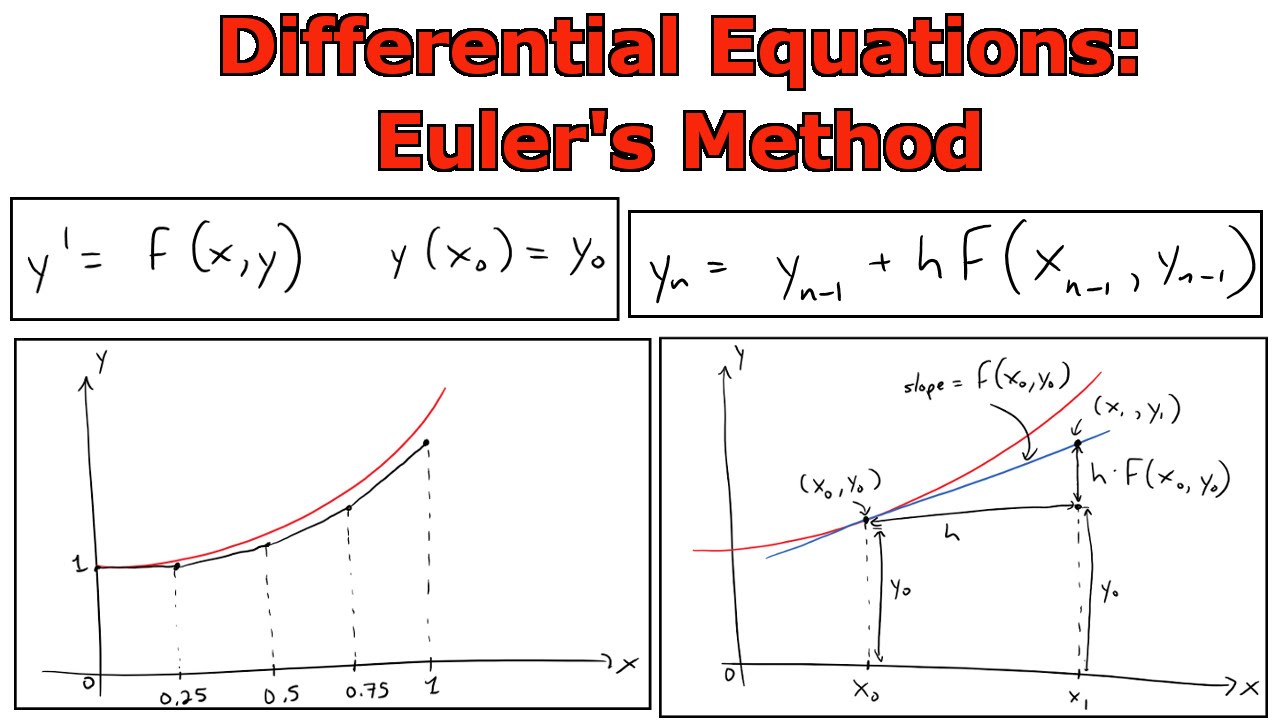
This way everything is anįinally put y, which is actualy y(0.1), then shift+return, and we have our nice answer.įirst, we start with output of our program, which is, perhaps, the most important Therefore we let y denote the actual value of y(x) when x = n*h. There is just one technical issue: we must have n as an For our example, we want to iterate 99 steps, so n will go from 0, 1, 2. The function of this Do loop is to repeat the expression, with n taking values from “starting number” to “ending number,” and therefore repeat the expression (1+ (ending number) - (starting number)) many times. (where usually \( a= x_0 \) is the starting point) into m equal subintervals For convenience, we subdivide the interval of interest Practical applications, it is almost always not a constant. In other words, we will find approximate values of the unknow solution at these mesh points.įor simplicity, we use uniform grid with fixed step length h however, in To start, we need mesh or grid points, that is, the set of discrete points for independent variable at which we findĪpproximate solutions. However, it is important to study because the error The process proceeds, so it requires a smaller step size. It has limited usage because of the larger error that is accumulated as Euler's rule serves to illustrate theĬoncepts involved in the advanced methods. Such as create a graph, or utilize the point estimates for other purposes. The user can then do whatever one likes with this output, Will be returned to the user in the form of a list of points. Numerical solution to the initial value problem for first order differential equation. Euler's method or rule is a very basic algorithm that could be used to generate a Where f(x,y) is the given slope (rate) function, and \( (x_0, y_0 ) \) is a Return to Part III of the course APMA0330 Return to the main page for the course APMA0340 Return to the main page for the course APMA0330

Return to Mathematica tutorial for the second course APMA0340 Return to Mathematica tutorial for the first course APMA0330 Return to computing page for the second course APMA0340 Return to computing page for the first course APMA0330